Community Detection

Community (or cluster) detection is procedure by which subnetworks are identified within the overall network. The subnetworks are cliques/clusters/communities of nodes that generally coactivate together.

Hierarchical Clustering

Sarah Muldoon recommended starting off with a hierarchical clustering of the adjacency matrix in order to visualize the structure of the matrix and get a sense of the sort of structure that exists within the data. The MATLAB help page for hierarchical clustering has some background information, but here are the highlights.

The first thing to note is that these steps are too computationally intensive for the adjacency matrices generated for the larger networks produced using the Lausanne 2008 parcellation (Lausanne 500 and 250 are too large). The myaparc_60 network seems to work smoothly; I'll try the 125 next.

Obtain Linkage

The first step of a hierarchical cluster is to obtain some kind of distance metric between each node in the graph. This information already exists in the form of the weighted adjacency matrices (either correlations or trained network weights). We pick up here at the linkage step. MATLAB has a linkage function that expects a vector of pairwise distances between all nodes, as would be generated by the pdist function. If you read the documentation for pdist, you will find that it outputs a vector for all pairs ({2,1}, {3,1}, ... , {m, 1}, {3, 2}, ..., {m, 2}, ... , {m, m-1}), where m is the number of nodes in the network. In relation to the adjacency matrices, these values would represent the lower (or upper) triangle of the matrix.

Filter Weights

The lower triangle of the adjacency matrix can be obtained in MATLAB using the tril function. An mxm (i.e., square) matrix has k diagonals, numbered 0 to (-1)*m-1. The main diagonal, k=0, will be the diagonal containing all ones (in a correlation matrix), which are meaningless in this context. We will want to get all the diagonals where k<0 (if you are getting the upper triangle using the triu function, use k>0).

mask=tril(ones(size(M)),-1); %identify the elements in the lower triangle, excluding diagonal k=0
lowert=M(find(mask)); %use mask to obtain the values.

The above code returns the values from the lower triangle of the adjacency matrix M as a vector in the same order that pdist generates.

Run linkage

There are several methods for running the linkage function, but common choices are single, complete, and average.

Z=linkage(lowert,'average');

Note that the solutions provided by each of these methods can yield drastically different results. For example, while I was working through this workflow for the first time, I used the single linkage distance calculation method. The sorted correlation matrix displayed at the end didn't seem to have any well-defined clusters of any size (leading me to assume that I had done something wrong). Since there doesn't seem to be any "correct" method, and the purpose of this exercise is to identify some sort of underlying structure to the weights, you might try different methods until you find something that makes that structure apparent.

Generate the Dendrogram

Using the dendrogram function, you'll need to force it to provide the entire leaf structure, specifying p, the maximum number of leaf nodes (if not specified, the default behavior is to display up to 30 leaf nodes):

[H, T, outperm] = dendrogram(Z, size(M,1));

Looking at the dendrogram can be used to inform the number of clusters you might look for in a data set (e.g., if something like k-means clustering was subsequently employed).

Sort and Visualize Adjacency Matrices

Outperm vector

Use the outperm vector generated by the dendrogram as a sorting index for the adjacency matrix to reveal the network clustering structure.

sorted_M=M(outperm,outperm); 
figure(2);
imagesc(sorted_M);

Simulated Annealing

This sounds fancy and tricky, but it's easily and quickly applied using the reorder_matrix.m function appearing in the Rubinov & Sporns (2010) Brain Connectivity Toolbox, which can be found in the ubfs Scripts/Matlab/BCT folder (file archive downloaded from the website, in the file BCT.zip).

[sorted_M, sortorder,cost]=reorder_matrix(M, 'line', 0);
figure(3);
imagesc(sorted_M);

In truth, the matrices generated by the simulated annealing method have more clearly visible modules than those generated by applying the outperm vector. I'm not sure why that would be, as the outperm vectors are a pretty transparent way of grouping related nodes together (unless the method described above has an error in it!).

Visualize Multiple Adjacency Matrices

Suppose you have several sorted adjacency matrices that you would like to display side-by-side. Use the subplot function to set up a grid-like organization of your figure:

subplot(2,2,1); %indexing within a 2x2 grid, the next thing you will be displaying will go in slot 1, which is the 1st row, 1st column
imagesc(sorted_run1);
subplot(2,2,2); %still in the 2x2 grid, the next displayed item goes into slot 2; slots increment by column within a row, until end of row is reached
imagesc(sorted_run2);
subplot(2,2,3); %3rd slot is the first column of the second row
imagesc(sorted_run3);
subplot(2,2,4); %4th slot is the 2nd column of the 2nd row
imagesc(sorted_run4);

This might be obvious to you, but when calling subplot(a,b,k) to visualize matrix K out of n total matrices, make sure that a × b ≥ n

Stochastic Clustering

A powerful and widely-used clustering algorithm is the Louvain greedy clustering algorithm. It's stochastic (i.e., contains a random element to it) because it's computationally intractable to completely search the entire space of possible clusterings for anything other than small "toy" networks.

The Louvain algorithm is described here, and has been incorporated in a collection of MATLAB network analysis scripts archived here and here but also stored in our ubfs Scripts/Matlab folder.

Create a Modularity Matrix

The first thing to note is that the genlouvain function doesn't work directly on the adjacency matrix, but instead on a modularity matrix, which is derived from your adjacency matrix. The number of partitions that are detected is influenced in part by a parameter, gamma, that is often omitted when this modularity matrix is calculated. When omitted, it defaults to 1, however larger gammas permit a greater number of final partitions. The following code sample is pulled from the genlouvain wiki site. The MATLAB function, full, transforms a sparse matrix into a full matrix. Sparse matrices are a more compact way of storing large data sets when there are a large number of empty values. I'm not clear whether the code works properly if the adjacency matrix, A, starts off as a full matrix, so instead I will begin by transforming the full matrix M (e.g., a 1000 x 1000 network) into a sparse matrix data type and proceed from there.

A=sparse(M);
gamma = 1.1; %gamma=1 tends to produce 3-community solutions. Higher values allow more communities.
k = full(sum(A));
twom = sum(k); %twom ("2m") is a normalization parameter 
B = full(A - gamma*k'*k/twom); %B is the modularity matrix

Detect Communities Using genlouvain

At this point, you now have B, the modularity matrix for the adjacency matrix M. Running the genlouvain function on B will stochastically generate a partitioning of your network that maximizes modularity (within its search space).

[S,Q] = genlouvain(B);
Q = Q/twom

Because this algorithm is stochastic, repeated applications of the genlouvain function are likely to generate somewhat different partitionings. Fortunately, the code runs rather quickly on relatively small networks, and so we can run the function repeatedly and store each partitioning.

maxiterations=10000; %how many partitioning attempts do you want?
S=repmat(NaN, maxiterations, length(k)); %preallocate storage for each partitioning solution
Q=repmat(NaN, maxiterations, 1); %preallocate storage for the modularity of each partitioning solution
for i=1:maxiterations
 [s, q]=genlouvain(B);
 q=q/twom;
 S(i,:)=s(:);
 Q(i)=q;
end

Determine the Consensus Best Partitioning

With maxiterations different partitionings of your adjacency matrix into different communities (stored in matrix S in the previous step), we can ascertain the consensus community assignment (i.e., the modal partitioning) for each node in the network. The commdetect toolbox has a function, consensus_iterative for that task.

[S2 Q2 X_new3 qpc] = consensus_iterative(S);

S2 is a matrix of size(S). mode(S2) can be used to list the representative partition for each node in the adjacency matrix, M. Most, if not all, rows of S2 will be the same, and mode(S2) will pick out the partitioning of S2 with the most votes. I haven't looked too deeply into the guts and math behind the code, but presumably the consistency among rows of S2 matrix will be reflected in qpc -- the quality of the consensus, where smaller values are better.

If you are working with multiple community partitionings of related networks (e.g., one network per run from the same participant within- or across-sessions), you might find it interesting to compare the consensus best partitionings to get a sense of the stability of these community assignments:

>> cbpart=squeeze(mode(S2))

cbpart = 

    1    1    1    1
    2    2    2    2
    3    2    3    3
    4    3    4    4
    1    1    5    1
    4    3    4    4
    ... etc.

There may well already be some analytic procedure that has been proposed and/or applied, and if one comes to light, it'll be described here. Until then, however, bear in mind that the community assignments are independent across the communities. For example, in the first line of the example output above, the first region was assigned to community '1' in all 4 adjacency matrices. However it is important to realize that community '1' in the first network may comprise an entirely different set of regions than community '1' in the second network. I expect that this potential discrepancy becomes more problematic with a greater number of discovered communities. Rather than look at what communities are assigned to each region, the correct thing to do is to look at what regions are assigned to each community. It is possible, for example, that community 1 in network A comprises the same regions as those belonging to community 2 in network B -- in this case, membership is perfectly consistent between the two networks for this particular community; it's merely the case that the community is labeled '1', in network A, and '2' in network B.

Visualize Communities

At this point you will have decided on the community assignments for each region in your adjacency matrix M. Let us suppose you have used the consensus best partitioning for a given network, and are storing these assignments in cbpart. At this point, if you had dropped any regions from your network, you will need to re-insert a placeholder value for those regions in cbpart:

% Assuming clustering was done on an adjacency matrix containing both hemispheres, 
% you will have to first split partition vector so that 
% you're only operating on the lh or rh regions
% The next line is for the myaparc_60 .annot file, which had 59 entries per hemi
% and dropped 2 regions (unknown and corpuscallosum) in each hemi
% This leaves 57 per hemi:
cbpart_lh=cpbart(1:57); 
% originally dropped regions 1 and 5 from the adjacency matrix
% we now have to insert placeholder values (cluster=0) for those two regions
cbpart_lh=[0; cbpart_lh(1:3); 0; cbpart_lh(4:end)]; 
%the resulting vector has a 0 inserted at elements 1 and 5 and is 2 elements larger
%Now cbpart_lh has 59 entries, which matches the number of entries in the
%original set of regions returned by parseFSSegments.m
%see also this link 

Generate a new CTAB file

The next step is to write out a color table file with the new rgb color assignments for each of the regions appearing in the .annot file (this is why we had to insert placeholder values for any dropped regions: If no entry if provided for these regions, this can be a problem). A MATLAB utility can be found in the ubfs Scripts/Matlab folder, called generateCTAB.m. When added to your Matlab path, you can pass this function your vector of community assignments and your region names. Be sure to read the help for this function, as there are a few other useful options, as well as the stipulation that the segID for the regions start at 0 and end at n-1 -- if this is not the case for your .annot file then you will have to provide a vector of segID values.

generateCTAB('classes', cbpart_lh, 'regions', lh_regions, 'prefix', 'lh_myaparc_60_clustered');

Create New Annotation File with New Colortable

After generating new color tables for each hemisphere, you will have 2 new .annot.ctab files (?h_myaparc_60_clustered.annot.ctab) in your current directory. The next step uses a hand MATLAB function called replace_ctab.m, written by Anderson Winkler (found in the ubfs Scripts/Matlab folder).

%assuming that the SUBJECTS_DIR environment variable is visible
subjects_dir=getenv('SUBJECTS_DIR');
subject_id='FS_T1_501';
labeldir=[subjects_dir filesep subject_id filesep 'label'];
source_annot=[labeldir filesep 'lh.myaparc_60.annot'];
new_ctab=[lh_myaparc_60_clustered.annot.ctab'];
new_annot=[labeldir filesep ...
                   'lh.myaparc_60_clust.annot'];
replace_ctab( source_annot, new_ctab, new_annot );

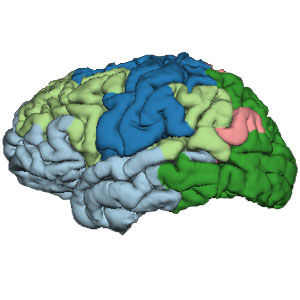
View Your Clusters

The communities within your network are easily visualized using your newly created .annot file in Freesurfer. From your terminal window:

SUBJECT_ID=FS_T1_501
LABELDIR=${SUBJECTS_DIR}/${SUBJECT_ID}/label
tksurfer ${SUBJECT_ID} lh pial -annot ${LABELDIR}/lh.myaparc_60_clust.annot