Mind Reading

The goal of so-called "mind reading" techniques is to use machine learning algorithms to decode brain states (as indexed by global patterns of cortical/subcortical activation) into their associated experimental conditions. Where this technique uses supervised learning, two things are required: First, a series of input patterns must be generated from fMRI activations. Second, a target pattern must be generated for each of the input patterns. This target pattern will indicate the experimental condition to be associated with each of the input patterns (e.g., REST (0) vs TASK (1)).

Determine Inputs

Source data for input patterns are obtained using the same methods used for connectivity analyses:

1. Load surface-space time series data (loadFSTS)
2. Remove any non-linear trends in the data (NLDetrendFSTS)
   • Note which, if any, rows you choose to drop from the data (e.g., it is customary to drop the first ~8-10 seconds of volumes from fMRI time series)
3. Normalize the time series data (normalizeMatrix)
4. Binarize and scale the normalized time series data (binarizeMatrix)

Determine Targets

Classifying Task vs Baseline Blocks

If the goal is simply to distinguish task block from rest periods, use findBlockBoundaries as follows:

%As mentioned above, keep in mind any samples dropped from the inputs:
droprows=[1 2 3 4]; %this vector was used in the call to NLDetrendFSTS;

sample_rate=2.047; %an fMRI study, with a TR=2.047 seconds
b=findBlockBoundaries([], sample_rate);
targets=zeros(1,b(end)); %1 zero for each volume -- default=baseline
for block=1:size(b,1)
 targets(b(block,1):b(block,2))=1; %block volumes get a '1'
end

targets(droprows)=[]; %remove from the schedule the dropped time points
%the first 4 × 2.047 seconds have been dropped from the schedule and from the input data
%as if this period never happened

It is possible that the number of samples in the input data may exceed the number of targets. For example, the experiment script may terminate at the 6:00 mark, but the neuroimaging may continue for an additional few seconds, ending at, say the 6:04 mark. Any input samples extending beyond the timestamp associated with the final target value obtained using the above method would be undefined, though they could be construed as being associated with non-task events. To avoid ambiguity, however, it might be advisable to drop input samples that were obtained after the last target.

Classifying Task Blocks

If blocks are associated with different tasks or conditions to be classified, the schedule vector, schedule can be created similarly, but with some modification. Here's some examples.

sample_rate=2.047; %each sample spans 2.047 seconds in this fMRI example
expinfo=load('LDT_Sub_1004_Run_11_18-Apr-2016.mat');
t=cell2mat({expinfo.data.timestamp});
vols=floor(t/sample_rate)+1; %convert the timestamps into volume numbers
cond=double(cell2mat({expinfo.data.conditon})); %what condition is each trial? 
%p.s., note the typo on "conditon"
b=double(cell2mat({expinfo.data.block})); %what block is each trial? 
bnums=unique(b); %what are the different blocks?
lookup=[0,1;0,2]; %condition codes that make up each block condition
bcodes=[1,2];%code assigned to each block condition
schedule=zeros(1,vols(end));%blank schedule preallocated for each volume

%%This loop will iterate through all the numbered blocks and use the lookup
%%table to determine which block code to assign each block, depending on
%%the individual trial conditions present in that block.
%%Then, all individual volumes that belong to that block will get assigned
%%that condition code. Anything not assigned a block code will remain '0'
%%(or 'rest'/'baseline')
for i=1:length(bnums)
   idx=find(b==bnums(i));%get indices of current block
   codes=unique(cond(idx));%what conditions are represented in this block?
   blockcondition=bcodes(ismember(lookup, codes, 'rows'));%lookup the blockcode (in bcodes) that matches the conditions in this block
   firstvol=vols(idx(1));
   lastvol=vols(idx(end));
   schedule(firstvol:lastvol)=blockcondition;
end

Event-Related Classification

The previous example would be used to determine targets for a network to be trained on uninterrupted tasks within a block design. In the case of a mixed or event-related design, jitter may be incorporated in between events of the same condition, and/or events of different conditions may be intermixed. The approach below is to initialize a vector of targets for each volume with zeros (for fixation) and set the task condition targets only for volumes with a trial associated with that condition.

samplerate=2.047;
t=cell2mat({expinfo.data.timestamp});
vols=floor(t/samplerate)+1 ;
vols=vols-4; %the first 4 volumes were dropped from the run
schedule=zeros(max(vols),1); %initialize a row vector of zeros: every volume associated with baseline unless otherwise indicated
cond=double(cell2mat({expinfo.data.conditon}));
%in this example, assume that there were 3 conditions, 0, 1, 2. We'll have to increment the values so that 0 still represents baseline
cond=cond+1;
schedule(vols)=cond; %use the volume numbers in vols to place the corresponding condition value into the correct slot in the schedule

Match Targets to Inputs

Input values will come from time series data, imported and scaled as described here. If any volumes have been discarded from the input time series, the same volumes will need to be deleted from the schedule of targets. Assuming we have a schedule and a set of inputs for a single run, we need to match each input vector to the corresponding condition in the schedule vector and produce a MikeNet example file. This will use a Matlab function, tentatively called mindReadingXFiles. As usual, calling help mindReadingXFiles will provide you with some usage guidance.

W=8;
CTIMES=[0 1];
OTIMES=[2];
PREFIX='C2D3';
P=1;
mindReadingXFiles('inputs', INPUTS, ...
   'targets', TASK_TARGETS, 'window', W, ...
   'clamp', CTIMES, 'output', OTIMES, ...
   'prolog', P, ...
   'prefix', PREFIX);

This function will generate one or more .ex files with the specified filename prefix. A sliding window is used to generate the examples in each file. A window size of w (4 is the default) will present w consecutive input patterns, on successive time steps (e.g., when the window is set to 4, the first example will present the first, second, third and fourth activation patterns; the second example will present the second, third, fourth and fifth activation patterns, etc.). The target for each input pattern is the corresponding row from the TARGETS vector. The clamp parameter sets the time steps that each input pattern needs to be clamped for, and the output parameter sets the time offset from the start of an input pattern presentation to check the output activation. This pattern is continued until the window is filled (e.g., the first input pattern is clamped for 0, 1, with targets on 2; the second pattern is on 2, 3 with targets on 4; the third pattern is clamped on 4, 5 with targets on 6; etc.). The output offset should be selected to allow for inputs in a multilayer network to have an opportunity to influence the output layer. Additionally, a prolog value, p can be used to instruct the function to present the initial p input patterns without setting associated target values.

Measuring Classification Accuracy

A testing module takes as input the continuous time-series for an entire run (i.e., with a window set to all) and generates an output value for each unit in the classification output layer for every time point in the example file. Note that the number of time points will likely exceed the number of volumes, effectively oversampling the time series. There is a mathematical relationship between the oversampling and the clamp/target parameters, but I'm not positive what it is just now.

Graphing Performance

Load the network output into a matrix, A. The first two columns contain information about the trial and the time point; the remaining columns contain the output activations, and there should be one column for each classification condition.

%Isolate output activations
Output=A(:,2:end);

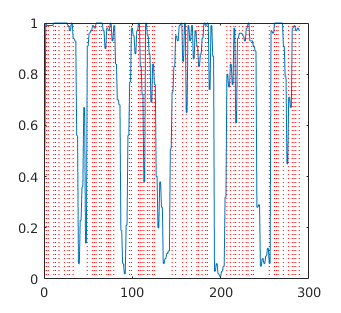
A visual indicator of network classification accuracy can be found by superimposing the volume onsets for each of the classification conditions. This can be done by using information from the schedule of TARGETS used to create the training file for the test data set (i.e., the matrix used by mindReadingXFiles.m) to create vertical indicator lines which are then superimposed on the network output plot. There are more than one MATLAB functions available on the MATLAB File Exchange. Two that I have tried are gridxy and vline.

Convert Schedule of Targets into Network Time Onsets

These steps are used to determine where each type of event occurred within the context of network time. Once you have the network timestamps, you can overlay the events on top of the network output time series. The example below shows how to determine where to plot the events associated with each volume in the test set

%%Obtain the events and timestamps associated with your test Exampleset
load('LDT_Sub_1004_Run_14_18-Apr-2016.mat'); %the data log for the run to be tested
sample_rate=2.047; %The sampling rate (TR) for this fMRI series
dropvols=4; %The first 4 samples were dropped from the time series data
t=cell2mat({expinfo.data.timestamp});
vols=floor(t/sample_rate)+1; %convert the event timestamps into volume numbers
vols=vols-dropvols; %Account for the initial dropped volumes

%%Convert sample timestamps into network time
%This will depend on the clamp/tdelay parameters used in the training/test example set
tstamps=(vols*2)-1; %Multiply the volumes by the clamp time and subtract 1 because the network is 0-indexed
conds=cell2mat({expinfo.data.conditon});%the vector of conditions associated with each event
onsets_0=tstamps(find(conds==0)); %when did the null events occur?
onsets_1=tstamps(find(conds==1)); %when did condition 1 occur?
onsets_2=tstamps(find(conds==2)); %when did condition 2 occur?

Plot Network Output Time Series and Overlay Event Onsets

Finally, the plot() function will plot a vector of network outputs, and vline() or gridxy() is used to overlay a vertical line where each event occurred. If plotting a continuous time series, the smooth() function can be used to eliminate the spurious noise that occurs in the oversampled network time series.

A=load('test.Early1.200000.gz.valid_Early_1.ex.txt');
figure(1);
plot(A(:,1), A(:,2), 'r-*', A(:,1), A(:,3), 'g-*', A(:,1), A(:,4), 'b-*');
gridxy(V2-1, 'Color', 'g', 'Linestyle', ':');
gridxy(V3-1, 'Color', 'b', 'Linestyle', ':');
gridxy(V1-1, 'Color', 'r', 'Linestyle', ':');

Training Notes

• Clamp noise is good for training and generalization, but too much noise makes it impossible to train
  • Interestingly, I've found the networks can train to criterion on the training set faster when noise is increased ... to a point
  • The utility of different noise thresholds surely depends on the granularity of the input range (i.e., the z-score threshold for 0 and 1) when scaling the brain activations
  • <0.2 is a good rule of thumb
  • Need to do some sanity check test networks to verify clampNoise (and possibly inputNoise) is working correctly
    • Unclear that new random noise is being generated on each forward pass, or that it's being applied where expected
• When training previously saved weights on concatenated training files, increase the -errd to a liberal value (e.g., 0.4) and train to get the net into the right ballpark
  • Once it's reached criterion, use more conservative error radius values, iteratively, if necessary
• Fixing the bias connections to the output to logit(errorRadius) (after weights are generated or loaded) seems to work so far